

The data has to follow a continuous or ordinal scale.Paired sample t-test (Displayed in the figure)Īs mentioned, the differences that make these t-tests different from the other tests are the assumptions of our experiment:.Unpaired two-sample t-test (Displayed in the figure).One sample t-test (Not displayed in the figure).The difference is the alternative hypothesis, as shown below. The statistical test can be one-tailed or two-tailed.

Important: It is always necessary to report the p-value and critical value. p_value between 0.001 and 0.01: Strong evidence.p_value between 0.01 and 0.05: Evidence.p_value between 0.05 and 0.1: Weak evidence.Therefore, with a critical value of 0.01, the results are more trustworthy but also more difficult to obtain. Reducing the critical value from 0.05 to 0.01 decreases the chance of a false positive (called a Type I error), but it also makes it more difficult to reject the null hypothesis. This 0.05 means that, if we run the experiment 100 times, 5% of the times we will be able to reject the null hypothesis and 95% we will not.Īlso, in some cases, statisticians choose ⍺ = 0.01. The critical value that most statisticians choose is ⍺ = 0.05. p_value ≤ ⍺ (Critical value): Reject the null hypothesis of the statistical test.
p_value > ⍺ (Critical value): Fail to reject the null hypothesis of the statistical test.However, since the p-value is just a value, we need to compare it with the critical value (⍺): The p-value is the variable that allows us to reject the null hypothesis (H₀: µ₁=µ₂) or, in other words, to establish that the two groups are different. The critical values of a statistical test are the boundaries of the acceptance region of the test. Also, there is the power of a test, defined as the probability of rejecting the nll hypothesis while it is false. The p-value or probability value is the probability of obtaining test results at least as extreme as the results actually observed during the test, assuming that the null hypothesis is true. The p-value and critical value are defined in Wikipedia as: What are the p-value and the critical value? Important: The t-test rejects or fails to reject the null hypothesis, never accepts it. If we want to examine more groups or larger sample sizes, there are other tests more accurate than t-tests such as z-test, chi-square test or f-test. This test should be implemented when the groups have 20–30 samples. If the t-test rejects the null hypothesis (H₀: µ₁=µ₂), it indicates that the groups are highly probably different.
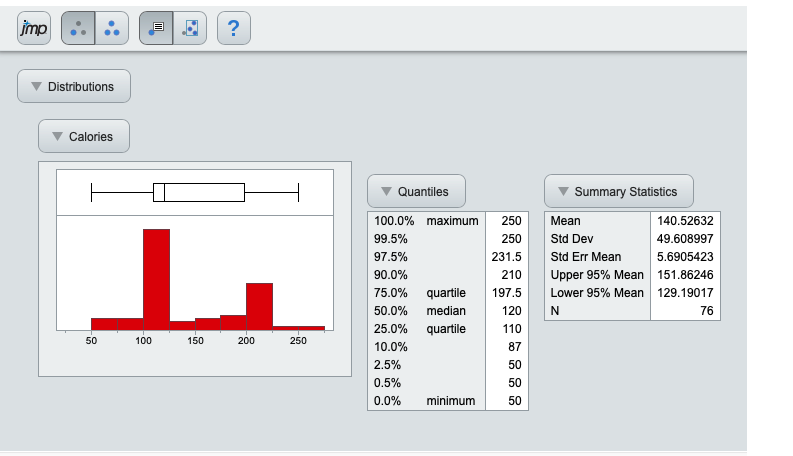
Mathematically, it establishes the problem by assuming that the means of the two distributions are equal (H₀: µ₁=µ₂). So, what is a t-test? It is a type of inferential statistic used to study if there is a statistical difference between two groups. This comparison can be analyzed by conducting different statistical analysis, such as t-test, which is the one described in this article.


 0 kommentar(er)
0 kommentar(er)
